1. 서론
당신의 친구가 자신은 초능력자이기 때문에 주사위를 굴려나온 결과를 90% 정확하게 예측할 수 있다고 주장한다고 가정하자. 당신은 이 사실을 믿을 수 없다. 이럴 경우 2개의 가설을 설정할 수 있다.
H1 : P(정확) = 1/6
H2 : P(정확) = 9/10
또한 친구가 10번의 주사위를 던져 9번을 정확히 예측했다는 D를 설정해보자.
이제 우도를 비교해보면(베이즈요인)
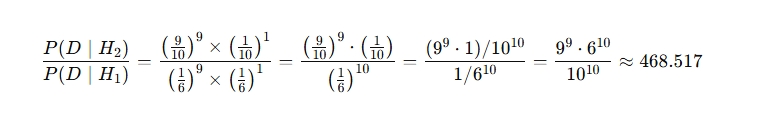
베이즈 요인 값은 약 468이 나오게 된다.
당신의 사전오즈 P(H2) / P(H1)이 이 베이즈 요인을 상쇄시킬 만큼 작지 않다면 당신은 이제 H2에 대해서 더 신뢰를 가지게 된다. 하지만 H2를 지지하는 데이터 D가 존재함에도 사람들은 여전히 H2를 믿지 않곤한다. 단순히 사전오즈를 상황에 따라 바꾸기 때문일까? 꼭 그렇지만은 않다.

2. 대립가설고려
H2를 지지하는 데이터가 나왔을 때 사람들은 사전 오즈를 바꾸기보단 새로운 대립 가설을 만든다. 이 경우 친구가 특정한 값이 나올 확률이 90% 정도인 가중된 주사위를 사용하는 것으로 믿게 될 수도 있다. 이 대립가설을 H3라고 해보자. H2와 H3의 사후오즈를 구해보면 다음과 같다.
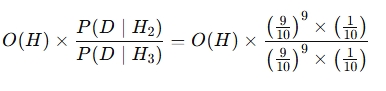
문제는 대립가설과 원가설의 오즈가 항상 1이 된다는 점이다. 즉 대립가설또한 원가설만큼이나 동일한 확률로 데이터 D를 설명하고 있으므로(즉 두 가설의 우도가 같음) 이럴 경우 사후오즈는 철저하게 사전오즈(사전신념)에 의해서만 결정되게 되어있다. 이것이 설득이 어려운 이유다. 사람들이 새로운 데이터를 보고 신념을 바꾸기 보다는 자신의 신념을 유지시켜주는 새로운 대립가설을 만든다는 것이다. 극단적으로 또다른 예시를 들자면
H4 : 친구가 나를 속이고 있다.
이러한 새로운 가설 H4를 도입시 사후오즈는 다음과 같이 계산된다.
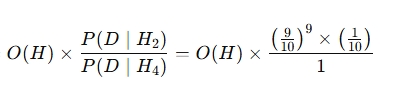
즉 이 경우 O(H) X 0.0386이 되어 오히려 베이즈요인 1보다 훨씬 낮은 값을 갖게 되어 상대의 신념을 바꾸기 더 어려워진다. 즉 애초에 상대방이 마음을 바꿀 생각이 전혀 없을 때 더 많은 데이터는 그들이 옳다는 것을 더 확신시켜 줄 뿐이다. 이렇듯 반증가능성을 배제하는 것은 과학이 아니라 미신의 영역이다. 따라서 굳이 그들의 생각을 바꾸기 위해 애쓸 필요가 없다.
'베이지안 통계' 카테고리의 다른 글
| 13. 몬티홀 문제 (0) | 2025.06.12 |
|---|---|
| 12. 모수추정 (0) | 2025.06.08 |
| 10. 사전신뢰의 강도 추정 (0) | 2025.06.08 |
| 9. 사후 오즈 : 아이디어 경쟁 (0) | 2025.06.06 |
| 8. 베이지안 A/B 테스트 설정 (1) | 2025.06.06 |



