
1. 서론
앞서 A/B 테스트를 통해 모수 추정의 문제를 가설 검정으로 바꾸는 법을 다루었다. 이번에는 거의 연속적인 범위의 가능한 가설을 살펴봄으로써 베이즈 요인과 사후 오즈(가설검정)를 모수 추정의 형태로 사용해 볼 것이다.
카지노에서 한 게임의 참가자가 다음과 같이 주장한다. "경품을 받을 확률이 1/2라고 종업원이 말한 이 게임의 실제 확률은 1/20에 불과하다. " 이에 대해 종업원이 항변한다. "아니다, 여전히 경품받을 확률은 1/2이다." 우리는 이를 다음과 같이 정리할 수 있다.
H1 : P(경품) = 1/2
H2 : P(경품) = 1/20
각 가설을 검정하기 위해 데이터 검정을 실시 했고 총 100번의 시행 끝에 24번의 경품을 수령할 수 있음을 확인했다고 가정하자. 즉 D가 이렇다는 것이다.
베이즈 요인
P(D | H1) = (0.5)^24 X (0.5)^76
P(D | H2) = (0.05)^24 X (0.95)^24
이를 토대로 베이즈 요인을 계산하면

값은 1/653 즉 약 0.00153이 나온다.
이 비율만 놓고 보면 종업원의 주장인 H1이 더 그럴싸한 가설로 보이지만 실제로 경품받을 확률이 0.5일 때 100회 중 24회의 경품을 수령할 확률은 매우 낮다.

이 값은 0.0000000629로 매우 낮다. 따라서 종업원의 가설도 신뢰하긴 어렵다. 상대적으로 고객의 가설에 비해 높은 가능성을 지닌 것 뿐이라는 것이다. 만일에 고객이 p = 0.2라고 주장했다면 고객의 가설이 훨씬 높은 우도를 가지게 될 것이다.

즉 이렇게 된다.
2. 더 많은 가설과의 비교
이제 종업원의 가설 H1을 고정시키고 더 많은 가설들과 H1의 우도를 비교해보자. 즉 수많은 베이즈 요인을 구해보자.
#--------------------
dx = 0.01
hypothesis = seq(0,1,by=dx)
bayes.factor= function(h_top,h_bottom){
((h_top)^24*(1-h_top)^76)/((h_bottom)^24*(h_bottom)^76)
}
bfs = bayes.factor(hypothesis,0.5)
plot(hypothesis,bfs, type='l')
#-------------------------------------------------------
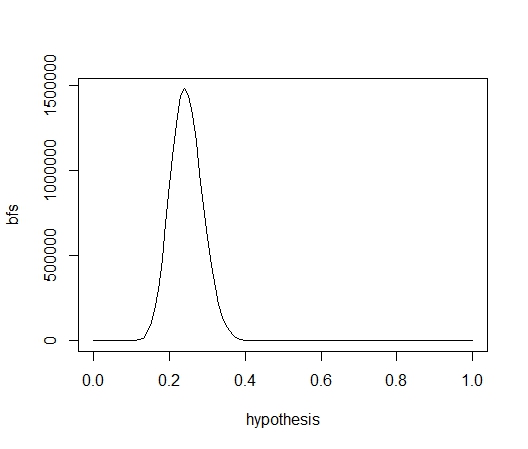
대립가설과 각 가설을 비교한 우도(베이즈요인)를 보면 이와같은 그래프가 생성된다.
3. 사전확률(사전신념)추가
만일에 이 게임의 제작자가 결코 당첨률을 0.2와 0.3사이에 두지 않았으며 이 범위안에 있지 않을 사전오즈는 1/1000이다고 말했다고 치자. 그렇다면 H2 중 p=0.2와 0.3사이에 위치한 가설에는 사전확률 0.001을 곱해줘야 한다. 나머지 경우의 사전오즈는 1이라고 하자.
#--------------
priors = ifelse(hypothesis>=0.2 & hypothesis <=0.3, 0.001, 1)
plot(hypothesis,priors, type='l')
#---------------
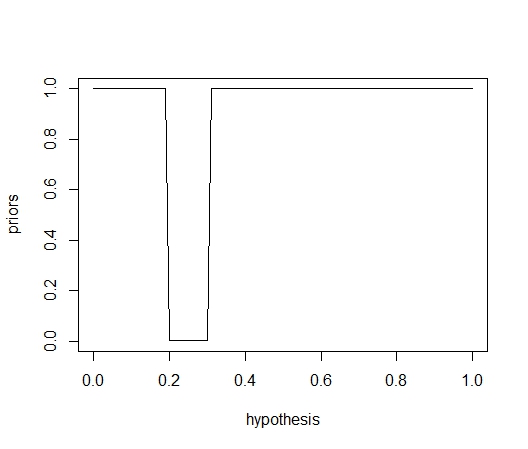
이 그래프는 사전 오즈의 분포를 나타낸다.
그렇다면 이제 사전 오즈 X 베이즈 요인을 통해 사후오즈의 분포를 구할 수 있다.
#--------------
posteriors = priors*bfs
plot(hypothesis,posteriors, type='l')
#---------------
결과는 다음과 같다
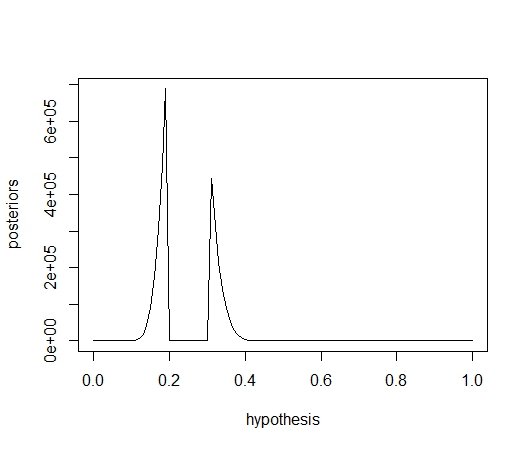
4. 확률분포 구축
진정한 확률분포는 가능한 모든 신념의 합이 1과 같은 경우이다. 따라서 위의 '사후오즈 X 가설에서 설정한 확률'의 총합이 1이 되도록 조정해보자
#-----------------
p.posteriors = posteriors / sum(posteriors)
plot(hypothesis, p.posteriors, type = 'l')
#----------------
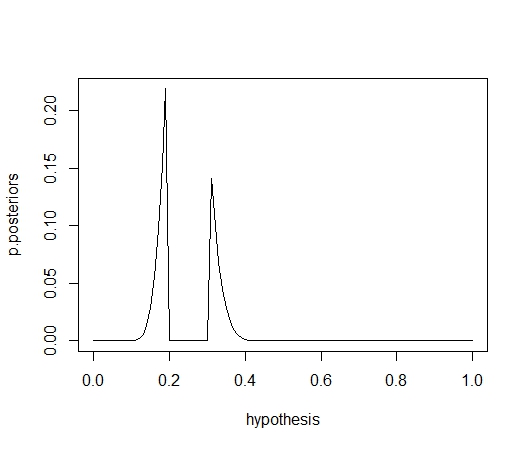
이제 각 가설에서 설정한 확률이 대립가설 대비 가지는 사후 오즈를 확률분포의 형태로 나타내는 데 성공했다. 이 분포에서는 우리가 실제 경품을 얻을 비율이 종업원이 주장한 것보다 적을 확률도 계산할 수 있다.
#----------------
sum(p.posteriors[hypothesis < 0.5])
#----------------
실제로 R에서 구동해 보면 0.9999995가 된다. 따라서 실제로 종업원이 경품 당첨 비율을 과장하고 있다고 확신할 수 있다. 또한 기대값과 가장 가능성이 높은 추정치를 구해보면
#--------------------------------
sum(p.posteriors*hypothesis)
hypothesis[which.max(p.posteriors)]
#-------------------------
0.24와 0.19임을 확인할 수 있다.
5. 베타분포와의 비교
앞서구한 베이즈요인의 분포를 살펴보자.

이는 beta(24, 76)과 상당히 유사한데 엄밀히 말하자면 beta(25, 77)과 동일하다.
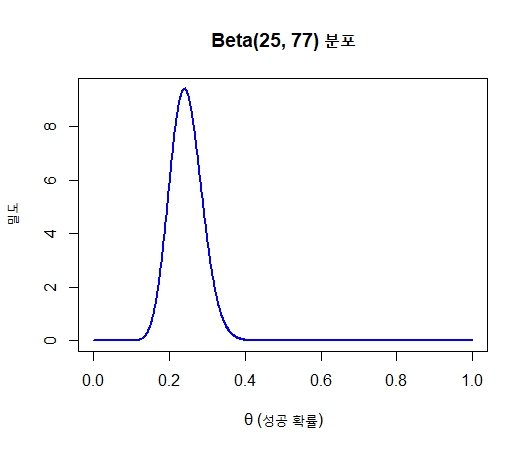
즉 베타분포 (24,76)에 사전신념 (1,1)을 결합하여 얻은 확률분포가 우리가 위에서 언급한 가설들의 분포(대립가설에서 p=0.5)와 같다는 것이다.




'베이지안 통계' 카테고리의 다른 글
| 13. 몬티홀 문제 (0) | 2025.06.12 |
|---|---|
| 11. 데이터로 상대의 신념을 바꿀 수 없는 경우 (1) | 2025.06.08 |
| 10. 사전신뢰의 강도 추정 (0) | 2025.06.08 |
| 9. 사후 오즈 : 아이디어 경쟁 (0) | 2025.06.06 |
| 8. 베이지안 A/B 테스트 설정 (1) | 2025.06.06 |



